

we will have to prove that angles opposite to the sides AC and BC are equal, i.e., ∠CAB = ∠CBA Proof: consider an isosceles triangle ABC, where AC=BC. Theorem 1 - “Angle opposite to the two equal sides of an isosceles triangle are also equal.” The angles formed between the base and leg ∠A and ∠C are called base angles The third side AC is known as the base, even if the triangle is not sitting on that side. Side AB is congruent to side BC therefore, we refer to those twins as legs. It also has three sides, and those are AB, BC, and AC Like any triangle, ABC has three interior angles those are ∠A, ∠B, and ∠CĪll three interior angles are acute angles.

Let us discuss some of the properties of an isosceles triangle. Here we have an isosceles triangle ABC to explore the parts. The angles opposite the two equal sides will always matchĪn isosceles triangle is called a right isosceles triangle when its third angle is 90 degrees. The triangle has two equal sides, with the base as the third, unequal side. Hence, length of AB = length of BC Some of the Basics About the Isosceles Triangle are as Follows: These are called legs if they are equal, it is an isosceles triangle. Here we have an isosceles triangle ABC, where side AB is congruent to side BC, which is the main reason the triangle is isosceles. The peak or the apex of the triangle can point in any direction. An isosceles triangle is known for its two equal sides.
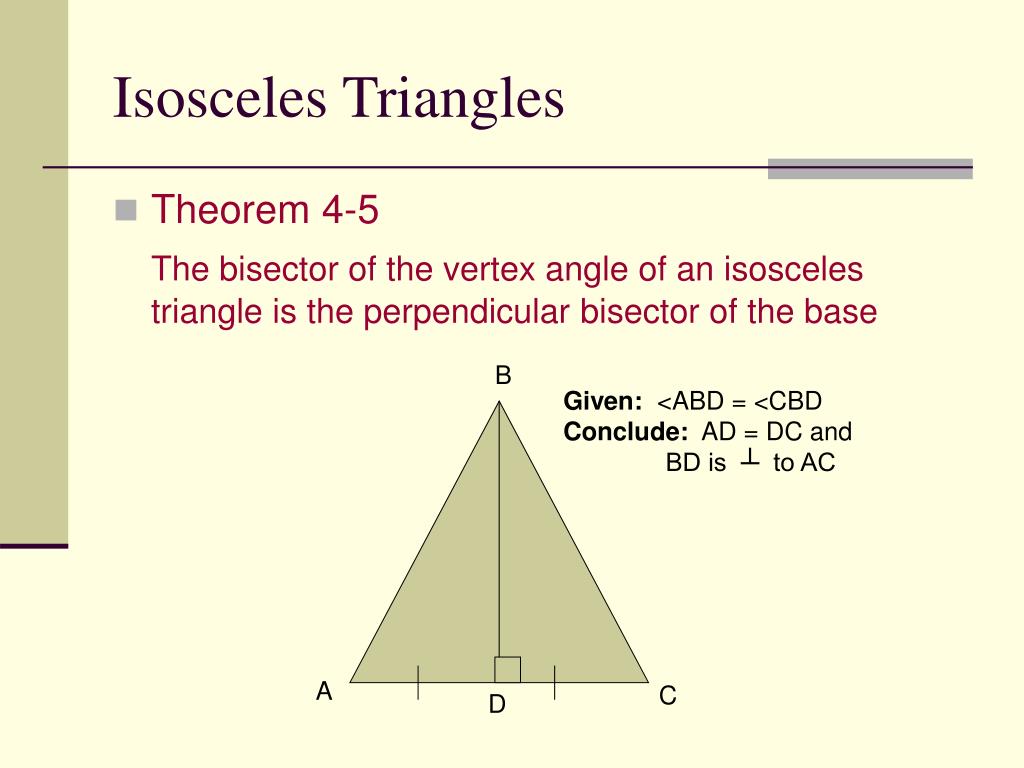
Today we will learn more about the isosceles triangle and its theorem.

Proof: This theorem is the converse of theorem-1. Theorem 2: The sides opposite to the equal angles of an isosceles triangle are equal. Therefore, the angles ABC and ACD opposite to the sides AC and AB respectively, are equal. In conclusion, ∠ABC and ∠ACD are the congruent parts of the congruent triangles, ΔBAD and ΔCAD. Therefore, ΔBAD ≅ ΔCAD by SAS congruency criterion. ⇒ To prove the above statement, we first draw a bisector that intersects the base at point D. To prove: Angles opposite to the sides AB & BC are equal i.e., ∠ABC=∠ACD Theorem 1 : The angles opposite to the equal sides of an isosceles triangle are also equal. The theorems for an isosceles triangle along with their proofs are as follows If the third angle is 90°, then it is known as a right isosceles triangle.All the angles are acute i.e., their measure is less than 90°.It has two equal angles that are the base angles (∠EDF and ∠EFD).A triangle that has two sides of equal lengths is called an isosceles triangle.


 0 kommentar(er)
0 kommentar(er)
